Thomas Havelka
Die Frage ob die beiden Komplexitätsklassen 
und 
zusammenfallen, oder ob eine echte Teilmenge von ist stellt eines der großen ungelösten Probleme der theoretischen Informatik dar. Der folgende Text bildet eine kurze Einführung in diese Problematik. Im Anhang gibt es eine kurze Liste von einführender Literatur, die sich mit dem = Problem, aber auch anderen Themen der theoretischen Informatik befaßt.
Informatik befaßt sich unter anderem damit, zu gegebenen Problemen Lösungswege oder Algorithmen zu finden. Komplexitätstheorie ist jenes Teilgebiet, das Probleme dahingehend zu klassifizieren versucht, welcher Aufwand an Zeit und (Speicher)platz zu deren Lösung mindestens benötigt wird. Zwei wichtige dieser Komplexitätsklassen sind und . So gehören Unifikation und Lineare Programmierung zur Klasse wohingegen das Travelling-Salesman-Problem und die Erfüllbarkeit der Aussagenlogik in - genauer gesagt in 
- liegen.
Als einfache Charakterisierung der beiden Klassen läßt sich sagen, daß die Klasse jene Probleme umfaßt, für die es Algorithmen mit vertretbarem Aufwand gibt, wohingegen für Probleme, die sind, solche Algorithmen nicht bekannt sind. Diese können nur mittels Approximationsverfahren gelöst werden. Andererseits konnte aber nicht bewiesen werden, daß es keine exakten Algorithmen mit vertretbarem Aufwand gibt.
Genau diese Problematik ist es, die durch die einfache Formel = beschrieben wird: gibt es für eine große Anzahl von Problemen exakte Algorithmen mit vertretbarem Aufwand (und ist es deshalb auch sinnvoll weiterhin danach zu suchen), oder gibt es diese nicht und die Probleme können nur möglichst gut approximiert werden.
Im folgenden sollen die beiden Klassen und sowie darin enthaltene Probleme beschrieben werden. Dazu werden zunächst werden Turingmaschinen definiert, welche die Möglichkeit bieten Probleme und ihre Lösungen zu beschreiben. Den Abschluß der Arbeit bilden einige Aussagen zum Aufbau von .
Turingmascinen stellen sehr einfaches Computermodel dar. Sie bestehen aus einem Lese- und Schreibkopf der sich stets in einem von mehreren Zuständen befindet. Dieser arbeitet auf einem in Zellen unterteilten, auf einer Seite endlosen Band. In jeder dieser Zellen steht ein Symbol - wobei es auch ein Leerzeichen gibt. Der Kopf befindet sich stets über einer Zelle.
Abhängig vom Zustand der Maschine und dem gelesenem Zeichen schreibt der Kopf ein Zeichen in die Zelle, bewegt sich eine Zelle nach links oder rechts (er kann auch stehenbleiben) und geht in einen neuen Zustand über.
Einige der Zustände zeigen an, daß die Berechnung beendet ist.
Formal ist eine Turingmaschine ein Quadrupel 
, wobei
der Startzustand ist.
enthält die speziellen Symbole 
- um eine leere Zelle anzuzeigen - und 
- zur Markierung des Ende des Bandes.
Die Übergangsfunktion ist folgendermaß definiert:
''halt'', ''yes'', ''no'' 
Eine Konfiguration (q,v,w) mit 
''halt'', ''yes'', ''no'' 
und 
beschreibt den momentanen Zustand einer Berechnung, wobei der Schreib- Lesekopf auf dem ersten Symbol von w steht.
Zunächst wird ein Wort 
auf das Band geschrieben. Die Turingmaschine M kann nun nach einer endlichen Anzahl von Schritten in einen der Zustände ''yes'' oder ''no'' kommen oder unendlich lange weiterlaufen. Dadurch wird eine formale Sprachen L definiert:
) oder M unendlich arbeitet (falls 
).
L ist nun die Menge jener Worte , für die M im Zustand ''yes'' anhält.
Natürlich läßt sich dieser Vorgang im allgemeinen auch umkehren, und zu einer Sprache L eine geeignete Turingmaschine entwerfen. Da man Probleme in Form einer formalen Sprache darstellen kann, sind Turingmaschinen geeignete Werkzeuge um diese Probleme (theoretisch) zu lösen.
Die Turingmaschine M wird auf Wort w mit der Länge n = |w| angewandt. Die Arbeit von M verbraucht Resourcen:
Es gibt einen funktionellen Zusammenhang zwischen n und dem maximalen m:
m = O(f(n))
Es sei z. B. 
. Alle Probleme, die sich mit diesem Zeitaufwand lösen lassen, werden zur Klasse TIME 
zusammengefaßt.
Alle Probleme, die sich mit polinomiellem Aufwand in Bezug auf die Länge des Inputs lösen lassen, werden nun zur Komplexitätsklasse der polinomiellen Zeit zusammengafaßt:
P 
TIME 
Auf die Gründe, warum Klassen mit verschiedenem polinomiellen Aufwand zusammengefaßt werden, soll an dieser Stelle nicht eingegangen werden. Der Leser sei an die am Ende angeführte Literatur verwiesen.
Zahlenematrix A, ein 
Vektor b (und ein 
Vektor c). Gibt es einen Vektor x, sodaß 
(und cx maximal)?
Verwendet man statt einer Übergangsfunktion eine Übergangsrelation so sind mehrere Folgekonfigurationen möglich. Stellt man die möglichen Verhalten dieser Turingmaschine graphisch dar, so erhält man einen Baum.
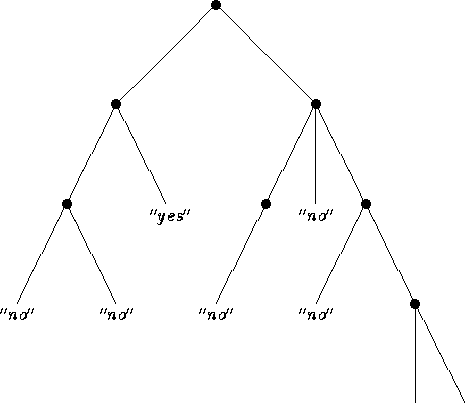
Jeder Zweig dieses Baumes kann:
Nun ist es nicht mehr so einfach zu sagen, was denn nun das Ergebnis einer Berechnung ist. Daher wird folgendes festgelegt:
Eine indeterministische Turingmaschine akzeptiert einen Input w, wenn mindestens einer der Zweige mit ''yes'' endet.
Genau wie bei deterministischen Turingmaschinen besteht auch bei indeterministischen ein Zusammenhang zwischen Größe der Eingabe und Dauer der Berechnung.
Hier betrachten wird die maximale Länge der Pfade, also die maximale Dauer der Berechnung. Diese sei durch O(f(n)) begrenzt. Daraus lassen sich nichtdeterministische Komplexitätsklassen ableiten:
NTIME(f(n)) sind alle jene Sprachen, die auf einer nichtdeterministischen Turingmaschine in einer durch O(f(n)) begrenzten Zeit entschieden werden können.
Analog zur Klasse bei deterministischen Maschinen, läßt sich auf nichtdeterministischen Maschinen die Klasse der nichtdeterministischen polynomiellen Zeit definieren:
NP NTIME
mit Gewicht 
und Wert 
eine Teilmenge 
wählen, sodaß 
und 
?
Neben den Turingmaschienen die Probleme entscheiden, die Berechnung also mit ''yes'' oder ''no'' beenden (falls sie dieses tun), gibt es auch noch Turingmaschinen, die einen Wert (ein Wort w) berechnen. Diese werden auch als Transducer bezeichnet. Bei der Problemlösung bietet das die Möglichkeit, ein Problem, zu dem man noch keinen Algorithmus kennt in ein anderes umzuformen, zu dem bereits ein solcher bekannt ist. Dabei ist natürlich auch möglich, daß die Umformung nur deshalb durchgeführt wird, weil man so einen effizienteren Algorithmus verwenden kann. Sinnvoll ist dieses Vorgehen natürlich nur dann, wenn der Aufwand zur Umformung vernachlässigbar klein ist.
Gegeben seien also zwei Probleme A, B mit den sie entscheidenden Turingmaschinen 
, 
. Des weiteren sei eine
Transformation R für alle 
definiert, sodaß 
. R wird als Reduktion bezeichnet, wenn gilt daß 
''yes'' gdw.
auch 
''yes''.
Gibt es eine solche effiziente Reduktion so sagt man:
Dies ist sinnvoll, weil der Aufwand zur Reduktion gegenüber dem Aufwand zur Problemlösung selbst vernachlässigbar ist. Das bedeutet, daß es keine bessere Lösung für A als für B geben kann. Gäbe es eine solche, so könnte sie ja auch für B verwendet werden, welches ja in ein äquivalentes Problem A umgeformt werden kann.
Formal schreibt man 
, wobei 
den Aufwand der Reduktion bezeichnet. Für Probleme in wird mittels 
(Logspace) reduziert. Die Klasse umfaßt alle jene Probleme, die nur logarithmischen Zwischenspeicher (im Bezug auf die Imputgröße) benötigen.
Wenn es um die Unterscheidung zu geht sind jedoch auch Reduktionen aus denkbar, da die Nacheinanderausführung zweier polynomieller Algorithmen ebenfalls polynomiell ist.
Das Problem B sei in einem Graphen die Existenz eines Hamiltonkreises zu überprüfen. Dies ist eine geschlossene Kantenfolge, die jeden Knoten des Graphen genau einmal enthält.
Das Problem A ist das Travelling Salesperson Problem mit Schranke D (TSP(D)). Dies bedeutet, daß nicht eine optimale Lösung berechnet werden soll, sondern überprüft wird, ob eine Rundreise mit bestimmetn Maximalkosten möglich ist.
Die Reduktion geschieht dadurch, daß die Kanten des ursprünglichen Graphen jeweils mit den Kosten 1 verbunden werden. Als Kostenschranke wird n, die Anzahl der Knoten vorgegeben.
Es ist leicht zu sehen, daß eine Lösung der transformierten Problems natürlich auch das ursprünglche Problem löst:
Der Nachweis, daß die Reduktion effizient ist, bleibt dem geneigten Leser überlassen.
Es stellt sich nun die Frage, ob durch die Verwendung von Reduktionen neue Erkenntnisse über Komplexitätsklassen gewonnen werden können. Wie wir sehen werden, ist dies der Fall. Doch zunächst soll der Begriff der Vollständigkeit eingeführt werden.
Gegeben sei ein Problem (eine Sprache) A und die Komplexitätsklasse C. Man sagt A sei vollständig für C wenn
gilt, und
auf A reduziert werden können.
Vor allem der zweite Punkt ist schwierig zu überprüfen. Hat
man jedoch ein vollständiges Problem so genügt es zu zeigen, daß dieses auf A reduziert werden kann. Da jedes Problem aus C auf B reduziert werden kann, kann es nun in einem weiteren Schritt auch auf A reduziert werden.
Durch die Definition einer Komplexitätsklasse ergibt sich meist auch ein für sie charakteristisches Problem, für welches gezeigt werden kann, daß es vollständig ist.
Das Problem 
, also die Erfüllbarkeit einer boolschen Formel ist das charakteristische Problem für . Der Beweis der Vollständigkeit ist im folgenden kurz umrissen.
liegt in , da man eine Variablenbelegung erraten kann, welche die Formel erfüllt. Dies entsprcht der Auswahl eines ''yes''-Zweiges im Ableitungsbaum. Die Überprüfung der Richtigkeit erfolgt in polynomieller Zeit, da auch der Zweig nur polinomielle Länge hat.
Des weiteren kann jede nichtderterministische Turingmaschine, welche ihre Berechnung für die Eingabe w in q(|w|) Schritten beendet, durch boolsche Formeln dargestellt werden. Im folgenden sei das Muster für die Formeln angegeben:
Der Ausdruck beschreibt folgende Elemente der Relation :
und 
bezeichnet den Zeitpunkt, zu dem eine bestimmte Konfiguration aufgetreten ist und 
bezieht sich auf die Position der Symbole am Band.
Für jedes Element Relation werden nun ausgehend von obigem Muster und die Werte 
Variable und dann eine boolsche Formel erzeugt, die das gesamte mögliche Verhalten der Turingmaschine beschreibt. Eine gültige Wahrheitsbelegung der Formel beschreibt nun einen Zweig der nichtdeterministischen Berechnung der Maschine.
Ergänzt man die Formel nun um eine Beschreibung des Eingabewortes und die Tatsache, daß die Maschine zu irgendeinem Zeitpunkt in den Zustand ''yes'' gelangen muß, so ist die Formel genau dann erfüllbar, wenn es eine Berechnung gibt, die mit ''yes'' endet.
Somit kann jedes Problem in auf reduziert werden und SAT ist somit .
in , so gilt P 
NP 
Im folgenden sind die drei Möglichkeiten dargestellt, wie die innere Struktur von aussehen kann.
liegen, noch sind.
sind entweder in oder .
= = .
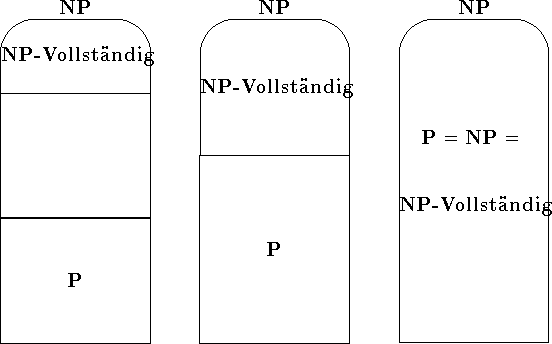
Es kann bewiesen werden, daß es Sprachen gibt, die weder sind, noch in liegen, falls und nicht zusammenfallen. Der mittlere dieser drei Pläne kann also nicht den Aufbau von beschreiben.
Welcher der beiden anderen richtig ist wird sicher noch jeden theoretischen Informatiker, der sich mit der Frage befaßt einiges Kopfzerbrechen bereiten.
Der Leser, der sich bis an diese Stelle durchgekämpft hat, sollte (hoffentlich) einiges gelernt haben. Er hat eine kurze Einführung in die Funktionsweise von Turingmaschinen erhalten. Mit Hilfe der Turingmaschinen wurden die beiden Komplexitätskalssen und beschrieben. Für beide Klassen wurden einige der in ihr enthaltenen Probleme beschrieben. Des weitern wurde die Methode der Reduktion als Methode der Problemlösung und der Begriff der Vollständigkeit zur genaueren Klassifizierung von Problemen eingeführt.
Es wurde auf den nicht akzeptablen Aufwand verwiesen, der (derzeit) mit der Lösung von Problemen der Klasse verbunden ist. Aus der Anzahl und Wichtigkeit dieser Probleme sollte sich erkennen lassen, warum die Frage ob = nicht nur für theoretische Informatiker eine große Rolle spielen, sondern warum auch Praktiker an diesem Problem interessiert sein sollten. Die Antwort auf diese Frage gibt schließlich Aufschluß darüber, ob gewisse Probleme (effizient) gelöst, oder nur approxomiert werden können.
= ?
This document was generated using the LaTeX2HTML translator Version 96.1-e (April 9, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 n-havelka.
The translation was initiated by Wolfgang Slany on Fri Jan 9 15:28:50 MET 1998